 Мало кто знает как именно работает асимметричное шифрование. К примеру есть люди которые не считают протокол https какой-либо адекватной защитой передаваемых данных. И как правило на попытку убедить в обратном, они отвечают что-то в духе «если мы передаем зашифрованные данные, то мы должны сказать как их расшифровывать, а эту информацию можно перехватить и, следовательно, расшифровать данные». А на аргументы, что это не так и в основу положено асимметричное шифрование, поступает ответ «Ну и что?».
Мало кто знает как именно работает асимметричное шифрование. К примеру есть люди которые не считают протокол https какой-либо адекватной защитой передаваемых данных. И как правило на попытку убедить в обратном, они отвечают что-то в духе «если мы передаем зашифрованные данные, то мы должны сказать как их расшифровывать, а эту информацию можно перехватить и, следовательно, расшифровать данные». А на аргументы, что это не так и в основу положено асимметричное шифрование, поступает ответ «Ну и что?».
Ладно, я понимаю, знать все тонкости реализации асимметричного шифрования нужно далеко не всем. Но общий принцип работы, я считаю, должен знать каждый, кто как-либо связан с компьютерами.
Хочу вынести суть данного поста в эту аннотацию: Запомните, асимметричное шифрование безопасно, естественно при выполнении всех условий. И чтобы доказать это я попробую описать алгоритм понятным языком, чтобы каждый смог понять, что он безопасен. Встречайте Алису, Боба и Еву и передачу их секретного сообщения под катом.
Кстати почему Алиса и Боб? Об этом есть кратенькая статья на википедии: Алиса, Боб и Ева. Чтобы было понятнее, Алиса и Боб хотят обменяться сообщениями, а Ева пытается эти сообщения перехватить и прочесть.
Немного истории
Криптография прошлых веков имела одну огромную проблему — проблема передачи ключей. В те времена существовали только так называемые «симметричные» шифры — шифры при котором данные шифруются и расшифровываются одним и тем же ключом.
К примеру, Алиса зашифровала некоторое сообщение и хочет отправить его Бобу. Естественно, чтобы Боб его прочитал, ему нужен ключ которым было зашифровано данное сообщение. И тут возникает проблема, как передать ключ чтобы его никто не смог перехватить. Пытливые умы предложат — пусть передают при личной встрече, а потом общаются сколько захотят. Да, не спорю, выход. А теперь представьте на секунду, что ваша интернет почта, перед тем как вы авторизируетесь в ней, потребует вашей поездки до физического местоположения сервера с почтой. Удобно? Пожалуй не очень.
Конечно ключ можно передавать по другому каналу связи. Но криптография рассматривает все незащищенные каналы связи как небезопасные. То есть передача ключа Бобу по телефону, например, считается небезопасной так, как ничто не мешает Еве прослушивать и телефон в том числе.
До 70-ых годов, эта проблема настолько стала привычной, что считался аксиомой тот факт, что для передачи сообщения нужно передавать и ключ которым сообщение зашифровано (причем некоторых люди до сих пор считают именно так). Но в 76 году Диффи и Хеллман предложили свой «метод экспоненциального обмена ключей». С этих годов и началось развитие асимметричных криптосистем.
Немножко реальной жизни
Прежде чем изучать какой либо алгоритм, нужно представить как он работает. И самый простой способ — это сравнить его с работой чего-то в реальности.
Представим что Алиса и Боб живут в стране, в которой вся почтовая система абсолютно аморальна и почтовые служащие читают всю незащищенную корреспонденцию. Алиса, девочка не глупая, прежде чем отправить сообщение Бобу, взяла железный ящик и, положив внутрь письмо и закрыв его на свой замок, отправляет этот ящик Бобу.
Естественно на почте прочитать это письмо не могут, но его не может прочитать и сам Боб, так как у него нет ключа которым закрыт замок. Алиса, конечно, может взять еще один железный ящик, положить в него ключ от предыдущего, и отправить его Бобу, но его Боб тоже не сможет открыть…
Единственный путь это все же сделать дубликат ключа и дать его Бобу при личной встрече…
И вот начинает казаться что обмен ключами является неизбежной частью шифрования — или все-таки нет?
Представим другую картину. Распишу пошагово:
- Алиса кладет свое письмо в железный ящик и, заперев его на замок, отправляет Бобу.
- Боб при получении ящика, (внимание!) берет свой замок и, дополнительно заперев им ящик, отправляет обратно.
- Алисе ящик приходит уже с двумя замками (напомню с первым замком Алисы от которого у нее есть ключ, и со вторым — Боба, от которого ключ есть есть только у Боба).
- Алиса снимает свой замок, и отправляет ящик обратно Бобу
- Бобу приходит ящик с уже одним его замком от которого у него есть ключ
- Боб отпирает оставшийся его замок своим ключом, и читает сообщение
Значение этой кратенькой истории огромно. Она показывает что два человека могут передавать секретное сообщение без обмена ключами. Вдумайтесь! Эта история фактически рушит все аксиомы на которых была построена тогдашняя криптография. Да мы получаем некоторое усложнение процесса (ящик пришлось пересылать три раза), но результат…
Вернемся к криптографии
Казалось бы решение найдено. Отправитель и принимающий шифруют свое сообщение, и затем собеседники поочередно снимают свой шифр.
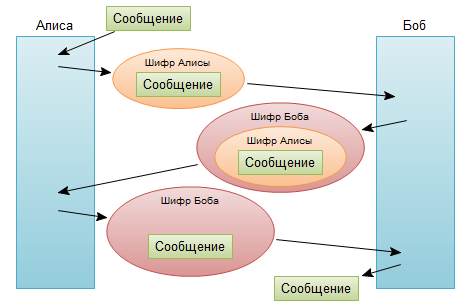
Но суть в том что не существуют таких шифров, которые бы позволили снять шифр из под другого шифра. То есть этап где Алиса снимает свой шифр невозможен:
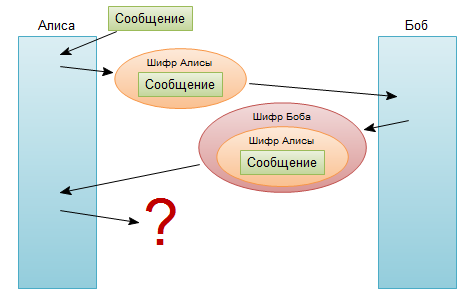
К сожалению, все имеющиеся алгоритмы до сих пор требуют снятия шифров в той очереди в которой они были применены. Боюсь назвать это аксиомой (так как история уже знает случаи когда такие аксиомы разбивались в пух и прах), но это так до сих пор.
Вернемся к математике
Идея с ящиком, о которой я описывал выше, вдохновили Диффи и Хеллмана искать способ передачи сообщения. В конце концов они пришли к использованию односторонних функций.
Что такое односторонняя функция? К примеру есть функция удвоение, т.е удвоить(4)=8, она двухсторонняя, т.к. из результата 8 легко получить исходное значение 4. Односторонняя функция — та функция после применения которой практически невозможно получить исходное значение. К примеру смешивание желтой и синей краски — пример односторонней функции. Смешать их легко, а вот получить обратно исходные компоненты — невозможно. Одна из таких функций в математике — вычисление по модулю.
За основу алгоритма Хеллман предложил функцию Yx (mod P). Обратное преобразование для такой функции очень сложно, и можно сказать что, по сути, заключается в полном переборе исходных значений.
К примеру вам сказали, что 5 x (mod 7) = 2, попробуйте найдите x, а? Нашли? А теперь представьте что за Y и P взяты числа порядка 10300.
Кстати сказать, для повышения стойкости, число P должно являться простым числом, а Y — являться первообразным корнем по модулю P. Но так как мы все же пытаемся понять теорию, то смысла заморачиваться на этом я не вижу.
Алгоритм Диффи-Хеллмана
И вот однажды Хеллмана осенило и он смог разработать рабочий алгоритм обмена ключами. Для работы по этому алгоритму нужно выполнять шаги на обоих сторонах, поэтому я зарисую это в таблице:
| Алиса | Боб | |
| Этап 1 | Оба участника договариваются о значениях Y и P для общей односторонней функции. Эта информация не является секретной. Допустим были выбраны значения 7 и 11. Общая функция будет выглядеть следующим образом: 7x (mod 11) | |
| Этап 2 | Алиса выбирает случайное число, например 3, хранит его в секрете, обозначим его как число A | Боб выбирает случайное число, например 6, хранит его в секрете, обозначим его как число B |
| Этап 3 | Алиса подставляет число A в общую функцию и вычисляет результат 73 (mod 11) = 343 (mod 11) = 2, обозначает результат этого вычисления как число a | Боб подставляет число B в общую функцию и вычисляет результат 76 (mod 11) = 117649 (mod 11) = 4, обозначает результат этого вычисления как число b |
| Этап 4 | Алиса передает число a Бобу | Боб передает число b Алисе |
| Этап 5 | Алиса получает b от Боба, и вычисляет значение bA (mod 11) = 43 (mod 11) = 64 (mod 11) = 9 | Боб получает a от Алисы, и вычисляет значение aB (mod 11) = 26 (mod 11) = 64 (mod 11) = 9 |
| Этап 6 | Оба участника в итоге получили число 9. Это и будет являться ключом. | |
Магия? Не спорю, с первого взгляда непонятно. Но после вчитывания и вдумывания в эту таблицу становится понятно как это работает. Впрочем если понятно не стало, то пролистайте до конца главы, там я выложил поясняющее видео.
Причем обратите внимание, что для получения ключа в конечной формуле, любому человеку нужно иметь три значения:
- Значения a и P, и секретное число Боба B
- или значения b и P, и секретное число Алисы A
Но секретные числа по каналу не передаются! Еве не получится восстановить ключ, не имея чьего-нибудь секретного числа. Почему — я писал выше, данная функция является односторонней. Попробуйте решите уравнение 4x (mod 11) = 2y (mod 11) найдя x и y.
Чтобы было понятнее, как работает схема Хеллмана, представьте шифр, в котором в качестве ключа каким-то образом используется цвет:
Допустим вначале, что у всех, включая Алису, Боба и Еву, имеется трехлитровая банка, в которую налит один литр желтой краски. Если Алиса и Боб хотят договориться о секретном ключе, они добавляют в свои банки по одному литру своей собственной секретной краски.
Алиса может добавить краску фиолетового оттенка, а Боб — малинового. После этого каждый из них посылает свою банку с перемешанным содержимым другому.
И наконец, Алиса берет смесь Боба и подливает в нее один литр своей секретной краски, а Боб берет смесь Алисы и добавляет в нее один литр своей секретной краски. Краска в обеих банках теперь станет одного цвета, поскольку в каждой находится по одному литру желтой, фиолетовой и малиновой краски.
Именно этот цвет, полученный при добавлении дважды в банки красок, и будет использоваться как ключ. Алиса понятия не имеет, какую краску добавил Боб, а Боб также не представляет, какую краску налила Алиса, но оба они достигли одного и того же результата.
Между тем Ева в ярости. Даже если она и сумеет перехватить банки с промежуточным продуктом, ей не удастся определить конечный цвет, который и будет согласованным ключом. Ева может видеть цвет краски, полученной при перемешивании желтой краски и секретной краски Алисы в банке, отправленной Бобу, и она может видеть цвет краски, полученной при перемешивании желтой краски и секретной краски Боба в банке, отправленной Алисе, но чтобы найти ключ, ей, на самом деле, необходимо знать цвета исходных секретных красок Алисы и Боба. Однако, рассматривая банки с перемешанными красками, Ева не сможет определить секретные краски Алисы и Боба. Даже если она возьмет образец одной из смешанных красок, ей не удастся разделить ее на исходные краски, чтобы найти секретную, поскольку смешивание краски является односторонней функцией.
Все равно непонятно? Тогда смотрим видео:
https://www.youtube.com/watch?v=5d8yniGL2G0
Что же, надеюсь, вы поняли, что существует вполне реальный способ безопасного обмена ключами. Но прошу заметить, назвать этот алгоритм асимметричным шифром пока нельзя, так как по сути это всего лишь алгоритм обмена ключами.
Асимметричное шифрование
асимметричный алгоритм предполагает под собой наличие двух ключей — публичного и приватного. То есть сообщение шифруется публичным ключом, а расшифровывается приватным и ни как иначе. Собственно именно эту концепцию сформулировал Диффи.
В общем суть данного алгоритма заключается в том, что принимающая сторона перед приемкой сообщения генерирует пару ключей на основе алгоритма модульной арифметики (принцип такой же как и в алгоритме Диффи-Хеллмана), собственно приватный и публичный ключ. Отправитель перед отправкой получает публичный ключ и шифрует сообщение данным ключом, после чего данное сообщение можно расшифровать только приватным ключом, который хранится в секрете у принимающей стороны.
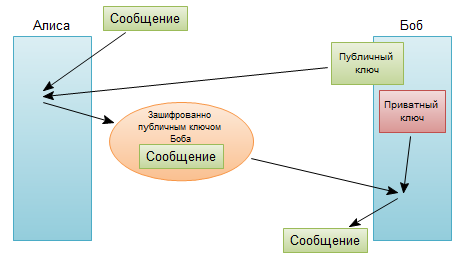
Если вернуться к аналогии с замками, то шифрование с открытым ключом можно представить себе следующим образом:
Любой способен запереть замок, просто защелкнув его, чтобы он закрылся, но отпереть его может только тот, у кого есть ключ. Запереть замок (зашифровывание) легко, почти все могут это сделать, но открыть его (расшифровывание) имеет возможность только владелец ключа. Понимание того, как защелкнуть замок, чтобы он закрылся, ничего не скажет вам, как его отпереть.
Можно провести и более глубокую аналогию.
Представьте, что Алиса проектирует замок и ключ. Она бдительно охраняет ключ, но при этом изготавливает тысячи дубликатов замков и рассылает их по почтовым отделениям по всему миру. Если Боб хочет послать сообщение, он кладет его в коробку, идет на местный почтамт, просит «замок Алисы» и запирает им коробку. Теперь уже ему не удастся открыть коробку, но когда коробку получит Алиса, она сможет открыть ее своим единственным ключом.
Замок и защелкивание его, чтобы он закрылся, эквивалентны общему ключу для зашифровывания, поскольку все имеют доступ к замкам и все могут воспользоваться замком, чтобы закрыть сообщение в коробке. Ключ от замка эквивалентен секретному ключу для расшифровывания, потому что он имеется только у Алисы, только она сможет открыть замок, и только она сможет получить доступ к находящемуся в коробке сообщению.
Есть несколько алгоритмов реализующих асимметричное шифрование. Самый известный из них — RSA. Расписывать его я не вижу смысла, так как понять как он работает с ходу все равно не получится, да и лучше чем написано на википедии я написать все равно не смогу.
Заключение
Что же, надеюсь что, поняв как работает асимметричное шифрование изнутри, вы станете больше ему доверять и соответственно чаще пользоваться SSL =)
Использовались материалы из книги Сингх Саймон — Книга шифров. Кстати, самая лучшая книга для тех кто хочет хотя бы чуточку разбираться в криптографии. Всем советую прочитать.
Позволю себе вставить ссылку на один из прошлых моих постов: Коллизии хеш функций? асимметричное шифрование решает! — пример «нестандартного» применения асимметричного шифрования.
Спасибо за внимание =)



эта картинка потерялась у вас
Спасибо за замечание починил картинки. Как вам статья в целом?)
прекрасная статья, всегда хотел прояснить эту тему
Видео не найдено :(
Буду очень благодарен, если выложите еще раз
Выложил еще раз) мои извинения
май 2018 — видео нет (
Замечательная статья! Огромное спасибо автору, так доходчиво и таким интригующим слогом я еще никогда не слышал, хотя учил и сдавал экзамен по RSA.
Побольше пишите по теме крипто у вас отлично получается!
Интригующим слогом?) Спасибо)
В этом рассуждении есть большущая дыра.
1.а. Почтальон вешает собственный замок и отправляет ящик обратно Алисе; кроме того, почтальон посылает точно такой же внешне выглядящий ящик опять же со своим замком Бобу
Дальнейшее, надеюсь, понятно)
«Дальнейшее, надеюсь, понятно» — тут нужно обязательно уточнить, что вы имели в виду, чтобы не отвечать на вопрос, который не задан.
«В этом рассуждении есть большущая дыра.» — а вот с этим уже можно поспорить.
Скомпрометировать переписку Алису и Боба невозможно, они получат ящики, которые не смогут открыть, если на них повесят замок. Если у Почтальона задача чтобы переписки не было, нужно взорвать ящик или выключить рубильник электричества — результат тот же.
Есть еще один момент, идея третей доверительной стороны. Это значит что на замках Алисы и Боба, будет еще «знак качества», потделать который почтальону можно только если он залетит внутрь еще одного ящика, находящегося может даже не на той же улице :)
Так Алиса поймет, если нужно, чей замок Боба, а чей нет.
Вполне себе может: 4.1 почтальон получает ящик со своим замком уже без замка Алисы и открывает его, то же самое и со стороны Боба, получая доступ к переписке. Основа атаки man in the middle, которая вполне себе работает в рамках приведенного алгоритма
Поэтому и сказано, что идея передачи с двумя замками — лишь идея.
Снять шифр из-под другого шифра нереально.
Хорошая статья, только видео не работает.
Спасибо, все очень понятно! Разложили по полочкам, читала с удовольствием!
Спасибо за статью.
Спасибо за заметку, очень образно, интересно и понятно. Мне как новичку теперь понятно что это такое и как оно работает. Еще раз спасибо.
Именно этого я и добивался. Спасибо и вам за комментарий =)
лучшее объяснение ассиметричного шифрования которое я встречал.
мне стало гораздо понятнее как это работает.
Спасибо большое.
И вам большое спасибо, мне приятно это слышать :)
Спасибо Вам, за интересную информацию изложенную в таком доступном для всех виде!
Замечательная статья, весьма доступно, спасибо!
А посоветовать книгу хорошую по основам криптографии и технологиям ssl/tls можете? :)
Спасибо и вам за отзыв!
По технологиям ssl/tls — не посоветую, т.к. не знаю таких. А вот по основам криптографии — я уже писал в статье:
Почитайте, там все более чем доступно, и читать ее приятно.
По-моему, Вы упустили один очень важный момент — процедуру передачи открытого ключа. Ведь его всё также нельзя передавать по открытому каналу. Иначе Ева сможет перехватить открытый ключ, передаваемый Бобом и отправить Алисе свой открытый ключ. Тогда Алиса будет шифровать сообщение открытым ключом Евы (думая, что это открытый ключ Боба), а Ева при перехвате сообщения от Алисы, будет расшифровывать его своим закрытым ключом, затем зашифровывать открытым ключом Боба и уже затем передавать дальше Бобу. Т.е. Ева сможет читать сообщения от Алисы Бобу.
Не скажу что я это упустил, пожалуй это уже следующая глава)
А данная атака называется MiTM. Так например Алиса, для защиты от данной атаки, в процессе установки соединения, предоставляет Бобу свой сертификат подписанный надежным центром сертификации , который подтверждает мол, что Алиса — та самая за которую себя выдает.
Из наиболее известного — так например работает HTTPS протокол. Грубо говоря, если клиенту передается самоподписанный (т.е. ненадежный) сертификат, то любой браузер выдает сообщение: «Мол данное соединение небезопасно или вас хотят прослушать». Но если сертификат подписан довереным центром — то это говорит о том что вы гарантированно подключены к нужному серверу.
Но для этого открытый сертификат центра сертификации должен быть передан Бобу заранее по защищённому каналу. Т.е. просто добавляется ещё один уровень шифрования, который никак не решает проблему безопасной передачи ключа без необходимости в физической встрече (или другом относительно надёжном способе передачи ключа). И утверждение:
неверно. А слова Вашего друга очень даже верны (если отнести их именно к проблеме в целом):
Я не спорю, в ваших словах есть правда, если говорить об ассимитричном шифровании в целом.
Но все же так или иначе на данный момент проблема решена. И решена она встраиванием доверенных корневых сертификатов в современные ОС.
И для этого владельцы корневых сертификатов должны передать их разработчикам ОС по защищённому каналу, а разработчики ОС должны передать свою ОС пользователю по защищённому каналу (чтобы злоумышленник не подменил в ОС корневые сертификаты). Улавливаете мысль? Я слишком категорично высказался, говоря что «просто добавляется ещё один уровень шифрования, который никак не решает проблему безопасной передачи ключа без необходимости в физической встрече». Я имел ввиду, что сама модель, подразумеваюшая передачу ключа по защищённому каналу (т.е. необходимость в физических встречах) никуда не делась, просто кол-во таких встреч сократилось для пользователя, но осталось неизменным для посредника (удостоверяющего центра) и второго действующего лица (который получает сертификат у удостоверяющего центра).
Паранойя — это конечно хорошо)
Ладно, хорошо. Я понимаю что Вы имеете ввиду. Но давайте все же отойдем от модели и теории и вернемся к реалиям. Про встраивание сертификатов в ОС — это всего лишь пример.
Основное правило работы с сертификатами:
Если это правило выполняется — значит можно утверждать что соединение безопасно. А реалии таковы что на данный момент корневые сертификаты распространены так, что, действительно, с этим поделать уже ничего нельзя.
Да и вообще, Вы несколько преувеличиваете опасность данной атаки.
Ну и повторюсь, эта статья о том «Как работает ассимитричное шифрование», а не о том о чем мы с Вами спорим. И описать все ньюнасы в ней я не смог. Прошу Вас, не надо ловить меня на том что я возможно не знаю про уязвимые стороны данного шифрования, цель написания статьи — совсем иная.
Я не пытался поймать Вас на незнании чего-либо, а всего-лишь хотел указать на некоторые некорректно сформулированные высказывания в статье, которые могут ввести Ваших читателей в заблуждение.
Открытый ключ можно и нужно передавать по незащищенным каналам. На то он и открытый (публичный). Только потом Алиса должна сверить с Бобом уникальный электронный отпечаток этого ключа. Если он совпал, значит ключ действительно принадлежит Бобу, а не Еве или кому-то другому. И личная встреча для этого вовсе не обязательна — это можно сделать по телефону или скайпу.
Я плохо разбираюсь в криптографии, но почему нельзя применить нижеследующий алгоритм?
1. Разбиваем шифруемую информацию на блоки. Каждый блок представлен числом. Размер блока (кол-во бит) определяет кол-во возможных значений блока и (соответственно?) стойкость шифрования.
2. Алиса для шифрования сообщения выбирает секретное число (которое никому не отправляет), которое прибавляет к каждому из чисел в блоках и отправляет зашифрованное таким образом сообщение Бобу.
3. Боб принимает зашифрованное сообщение, выбирает своё секретное число (которое также никому не отправляет), прибавляет это число к каждому из чисел в блоках зашифрованного Алисой сообщения и отправляет это двукратно зашифрованное сообщение Алисе.
4. Алиса вычитает своё секретное число из каждого числа в блоках этого двукратно зашифрованного сообщения и отправляет получившееся сообщение Бобу.
5. Боб вычитает из этого (уже однократно зашифрованного) сообщения своё секретное число и получает исходное расшифрованное сообщение Алисы.
Пример на PHP:
$message = array(154, 125, 113); $secretKey1 = 54; // Ключ Алисы $secretKey2 = 234; // Ключ Боба print implode('|', $message) . "\r\n"; foreach ($message as $key => $block) $message[$key] = $block + $secretKey1; print implode('|', $message) . "\r\n"; foreach ($message as $key => $block) $message[$key] = $block + $secretKey2; print implode('|', $message) . "\r\n"; foreach ($message as $key => $block) $message[$key] = $block - $secretKey1; print implode('|', $message) . "\r\n"; foreach ($message as $key => $block) $message[$key] = $block - $secretKey2; print implode('|', $message) . "\r\n";Однако, хочу заметить, что проблему безопасной передачи ключа этот подход также не решает. Если вернуться к аналогии с железными ящиками, то Ева может перехватить сообщение нижеследующими способами.
Скрытый перехват и/или подмена сообщения с задержкой во времени:
Подмена сообщения без задержек во времени:
Скажу чесно, я тоже не криптограф, всего лишь немного увлекаюсь. Но вроде как звучит вполне убедительно. Патентуйте) Пойду на бумажке распишу/прикину что к чему.
А по поводу вариантов перехвата сообщения — вобщем то вы опять описали классическую атаку MiTM
Ну да, это снова был камень в огород утверждения о том, что «два человека могут передавать секретное сообщение без обмена ключами» :)
Ладно, сдаюсь)
Будем считать что я вкладываю в эти слова немного другой смысл =)
Простое сложение-вычитание/xor-xor не запатентуешь. Этот прием не является никаким особым изобретением.
Короче. Ева перехватывает зашифрованное сообщение Алисы(message_one). Далее пересылает его Бобу без каких либо модификаций.
Боб добавляет свой ключ к зашифрованному сообщению Алисы. Ева перехватывает зашифрованное сообщение Боба и сохраняет у себя, после чего пересылает его Алисе без модификаций(message_two).
Далее Ева просто вычитает одно сообщение из другого (message_two — message_one), тем самым получает ключ Боба, в чистом виде. После чего ей нужно лишь перехватить последнее третье сообщение от Алисы, которое будет лишь зашифровано ключом Боба, который теперь Ева уже знает.
Алиса шифрует своё сообщение, после чего передаёт Бобу.
Боб шифрует своё сообщение, после чего передаёт Алисе.
Вот в этих двух передачах по середине участвует Ева которая просто сохраняет два сообщения. После чего она вычитает из второго первое, что ей даёт ключ Боба в чистом виде…
Да все верно. Где то это у меня тут уже писали :)
Да и я где то читал статью зарубежную где доказывалось что стойкое шифрование снимать не в той очереди в которой оно было наложено не выйдет. Либо же это шифрование является нестойким.
А статью или хотя бы наводку для поиска можно?
Боюсь, что нет. Я прочитал, запомнил, да и ушел дальше… а где и даже когда… к сожалению, не помню
Я собрал ваш алгоритм в Java и нашел его уязвимость. Правда, я раскладывал сообщение на массив char и преобразовывал их в ASCII коды, а затем добавлял секретные числа. Ваш метод — не криптография, а её иллюзия. Вы добавили один два лишних шага, которые хакер может спокойно убрать. Взлом:
1. Взять зашифрованное (двумя ключами или одним, не суть важно) сообщение.
2. Разложить на биты (или ASCII код, как в моем случае).
3. Начать перебор чисел.
4. Можно вручную смотреть результат и отделять бред от осмысленного сообщения, можно запустить после каждого перебора поиск по словарям, а можно натаскать нейросеть (я за вариант со словарями).
С современными мощностями на это уйдут минуты, в лучшем случае часы. Ваш алгоритм не безопасен и не подходит для секретного обмена данными… А жаль, идея была хороша.
То что вы описали — называется брутофорс атакой. Любая система/механизм/шифр уязвимы к ней. Считается что шифр надежен, если расшифровать сообщения вы можете только с помощью полного перебора ключей (брутофорсом), т.е. тем что вы описали у себя комментарии.
В реальном алгоритме Диффи Хелмана, используются ключи минимум в 512 бит, а это число с где-то 150 нулями (см тут я это писал).
Подбор такого ключа у вас займет времени ну оооочень много. Чуть больше чем существует вселенная. Даже на очень мощных компьютерах.
Для чего нужна эта ахинея с открытыми ключами? Симметричные надёжней.
Добрый день!
Хороший сайт, понятно изложен материал, огромное спасибо автору. Попал сюда случайно в сентябре, когда искал информацию по практическому шифрованию.
Пишу потому, что хочу спросить: Есть желающие узнать как найти числа для симметричного шифрования? Могу научить на пальцах как быстро проверить число Р на простоту (без поиска числа g) — но это вряд ли будет интересно. Самое интересное:
Найти число Р любой длины и число g к нему. Никакие 2 в степени n плюс один (или минус один) при этом не использую. Естественно, это бесплатно. Есть даже сайт, где я выложил свою работу.
Симметричный не надежнее ничуть. Да и вообще симметричный/ассиметричный — это разная идеолгоия шифрования. То же самое если бы вы сравнивали кофемашину и посудомойку. Они выполняют разные функции.
Огромный минус симметричного шифрования — ключ для шифрования должен быть передан по защищенному каналу обоим сторонам. Не всегда такой канал и такая возможность есть. Ассиметричный — лишен этого недостатка.
Нет симметричное шифрование менее надежное так как увеличивает вероятность взлома вдвое. Ну например к Алисе придут зеленые человечки и применят метод терморектального криптоанализа, то всё пропало, всё раскрыто!. В случае с ассиметричным шифрованием с участием пары публичного-приватного ключа (которое, кстати, здесь не описано) зеленые человечки должны будут придти к тому у кого приватный ключ. Соотвественно, рассекретится только часть системы.
Понимаю что прошло много времени, но все же отвечу для таких же как я новых читателей.
Это не сработает, т.к. после действий 2 и 3 мы видим разницу, на которую изменилось число каждого из блоков, следовательно нам становится очевидно секретное число Боба и нам остается только перехватить сообщение после 4-го действия (т.е. уже без шифра Алисы) и воспользоваться уже известным нам числом Боба.
Огромное спасибо за статью!
После прочтения почти все легло на свои полочки, обрело структуру, которую легко наращивать.
Имея такую структуру легко генерировать правильные вопросы (полочка для атак MiTM, отдельное спасибо Михаилу :)).
С точки зрения педагогики Вы сделали все идеально. Думаю Вы правы, что не добавили в эту статью атаки MiTM иначе был бы перегруз информационный.
Видео прелестное, особенно учитывая его возраст.
PS: использование метафор для объяснения «сложных» систем честно говоря трудно переоценить. Еще раз спасибо!
И вам огромное спасибо за ваш комментарий =)
Мне очень приятно слышать что мои статьи кто-то читает и то что кому-то они помогают)
Из этой статьи я не уловил момент перехода от алгоритма Диффи-Хеллмана, где два абонента для получения секретного ключа обмениваются публичными данными и промежуточными результатами вычислений (в примере получилось целых 6 этапов) к тому этапу, где для шифрования используется некий публичный ключ, который затем дешифруется при помощи приватного (я здесь насчитываю всего 2 этапа передачи данных — отправка публичного ключа и отправка зашифрованного этим ключом сообщения).
Т.е. я понимаю, что где-то между двумя этими объяснениями наверняка кроется много математики, и в итоге объяснение сводится к «это работает именно так, просто поверь». Но было бы наверное проще понять этот внезапный переход, если бы аналогию с красками распространили на объяснение сути шифрования публичным ключом с последующим дешифрованием приватным. А пока получается какое-то «Б работает потому-что А», в то время как между А и Б чёткой связи не прослеживается. По крайней мере для меня.
Уважаемый автор, не будете ли вы так любезны пояснить мне сей мистический прыжок от А к Б? :) Спасибо!
Сразу же попробую сам себе всё объяснить :)
Я пытаюсь провести аналогию с красками… Если я понял правильно, то отправка публичного ключа — это и есть отправка уже замешанной смеси цветов, где есть и заранее оговоренные цвета, и секретный цвет, который добавляет автор. В то же время приватный ключ — это просто рецепт, который хранит список использованных цветов.
Ну и опять же, если я правильно понимаю, отправка сообщения, зашифрованного публичным ключом, это процесс подмешивания совершенно любого цвета в полученную смесь красок таким образом, что цвет этой смеси не меняется. Соответственно, при «разделении цветов» приватным ключом (читай — рецептом) мы можем вычленить этот подмешанный цвет.
Что-то я сам себя уже запутал… :) Или я всё представляю верно?
Попытка понять аналогию с цветами возможно покажется вам наивной, но если уж мы её выбрали для разъяснений, то давайте использовать её до конца для объяснения перехода от одной концепции к другой (т.е. от алгоритма Диффи-Хеллмана к публичным и приватным ключам) :)
Да, перечитал статью… вы верно подметили.
Чесно говоря, вот так сходу не могу представить себе это на аналогии с красками. Я подумаю как это будет выглядеть и постараюсь дополнить статью =)
Спасибо за замечание =)
Всегда пожалуйста!
Вам спасибо за статью, всё же материал годный, добавил в закладки ;)
Ну а если не с красками… Возьмём нашу формулу «Y^x (mod P) » и применим её к публичному и приватному ключам. Как взаимосвязаны ключи и параметры X, Y, P; и в какой момент передаются Y и P (и передаются ли) ? Так уловить суть было бы даже проще… наверное.
Ещё раз спасибо!
Добрый день,
Дано: есть формула Y^x (mod P).
пример в статье основывается на формуле 7^x (mod 11)
я взял для своего примера 4^x (mod 7)
и у меня не получилось прийти к общему ключу.
Вопрос: почему алгоритм в примере работает для 7^x (mod 11) и не работает для 4^x (mod 7)?
Работает же, внимательнее в расчетах. Вот взял вашу формулу:
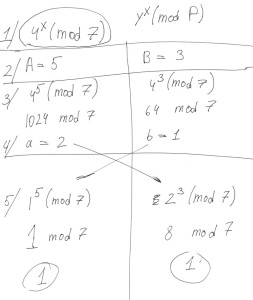
PS: сори что вот так коряво) набросал на листике, это скан с него. Лениво набирать формулы сюда, но и так то тоже все понятно.
Пасиб. работает ошибься
я для проверки стал пользоваться гуглом — прямо в строке поиска можно писать
4^3 mod 7
Это замечательная статья! Автору большое спасибо. читается на одном дыхании.
Пишите еще — радуйте людей)
Спасибо, статья отличная!
Только вот чуть не разобрался в алгоритме, в том, как высчитывать через модуль.
Не подскажите, как высчитывать число В, если число А меньше модуля?
Ну например:
3(mod 13) = ?
Я знаю, что если, например, нужно высчитать 625(mod 13), нужно 625/13, а потом наибольший возможный целый делитель (48) умножить на модуль (что здесь будет равняться 624), и наконец 625-624 = 1
Числа 625 и 1 сравнимы по модулю 13, так как 624 делится на 13.
Вот это я понимаю. А вот как быть если модуль больше числа а?
Гм… подразумевается немного более простая операция — остаток от деления. Так например остаток от деления 625 на 13 равен 1. А остаток от деления 3 на 13 равен 3. Ну или может чтобы понятнее было:
И т.д.
Автор, спасибо за статью. Только пожалуйста, измени «преобразование по модулю» на «остаток от деления», когнитивный диссонанс получается пока читаешь :(
CTRL + F по этой фразе ничего не дал)
Но как бы это и так и так правильно.
1. Атака «человек посередине», это серьёзная проблема. Насколько я могу судить, в рамках одной только криптографии она в принципе не решается: если принять, что Ева способна перехватить и незаметно подменить ВСЕ данные, поступающие к Алисе или исходящие от неё по ЛЮБЫМ каналам связи, никакое шифрование не поможет. Как минимум один сертификат должен быть получен Алисой из абсолютно надёжного источника. Но в случае, если злоумышленник может только прослушивать канал связи, а не менять данные в нём, асимметричное шифрование вполне надёжно.
2. Что касается возможности снимать один «слой шифра» из-под другого, этим свойством обладает банальная функция XOR, широко используемая в криптографии с древнейших времён по сей день. Не думаю, что её можно запатентовать :(
Да вы правы, атака mitm на сегодняшний день не решается никак если быть абсолютным параноиком. Если же им не быть то возня с сертификатами и подписями обеспечивают «необходимую и достаточную» защиту.
Что касается функиции XOR — ее сложно назвать шифром, т.к. им она по своей сути не является.
Да ладно? Погуглите про «Шифр Вернама». Это система передачи сообщений с абсолютной криптоустойчивостью. И основана она именно на XOR. Если оставить в стороне некоторые организационные сложности (создание истинно случайных ключей с равномерным распределением, сохранение тайны шифроблокнота в недружелюбном окружении и надёжное уничтожение использованных ключей), ничего проще и надёжнее человечество ещё не придумало.
Да ну бросьте, о какой абсолютной криптоустойчивости вы говорите?
До тех пор пока длина ключа меньше длины шифруемого послания, любой шифр не будет абсолютно криптоустойчивым. Мы же все же говорим о таких шифрах? Единственное что придумал Верном — использовать, грубо говоря, бесконечный ключ, что собственно и дает устойчивость. Ну и к слову сказать ни капельки не абсолютную, если мне не изменяет память, даже он не реализовывал бесконечность в своих ключах, ленты с ключами в его аппарате были зациклены.
Ну а так да, конечно, если мы будем использовать ключи длинее текста, то любой шифр становится абсолютно устойчивым.
По проекту Вернама, каждая лента должна была использоваться однократно и после этого уничтожаться. Идея закольцевать ленты была выдвинута кем-то другим уже в ходе практической эксплуатации прибора, ради экономии.
Нет, не любой. Для достижения абсолютной криптоустойчивости методом Вернама (думаю, и любым подобным) нужно три равноважных фактора:
1. Ключ не короче сообщения.
2. Ключ состоит из истинно случайного набора символов с равномерным распределением.
3. Ключ никогда не используется повторно.
Нарушение любого из них резко снижает криптоустойчивость.
Остальные правила подразумевались само собой. Ну а так да, спорить не буду.
Хотя, по здравом размышлении, я понял, что метод с двойным обратимым шифрованием не работает, если злоумышленник знает алгоритм шифрования. Рассмотрим на примере идеи Михаила:
Пока всё в порядке: Ева не может прочесть сообщение Алисы, т.к. не знает число-ключ. Если блоки достаточно велики, восстановить сообщение Алисы сложно, а если блок длиннее сообщения и ключ не имеет уязвимостей — невозможно. Но Ева может скопировать шифрограмму Алисы и делает это.
А вот тут уже начинаются проблемы: Ева всё ещё не может прочесть сообщение Алисы, но, располагая копией полученной Бобом шифрограммы и отправленной им двойной шифровкой, без проблем восстанавливает ключ Боба.
Алиса сняла свой «слой» шифра и теперь пересылает Бобу своё письмо, зашифрованное только ключом Боба. Который у Евы уже есть! Ева расшифровывает письмо и читает его, а также на всякий случай может восстановить ключ Алисы, пользуясь расшифрованным текстом письма и первой перехваченной ею шифрограммой.
Да, действительно. Все верно. Подобная цепь рассуждений мне пришла в голову немногим позже, а еще чуть позже я ее и забыл, не успев написать здесь))
Но вы правы, некоторые из шифров допускают восстановление ключа из исходного текста и зашифрованного текста. Поэтому пересылать эти данные нельзя.
Здравствуйте. Хорошая статья, но я тоже не понял некоторые моменты, которые описали выше.
Именно переход от алгоритма получения секретного ключа обоими собеседниками (Алиса и Боб) (без их выкладывания в публичный доступ) к асимметричному шифрованию.
У вас написано, что сообщение кодируется на стороне Алисы публичным ключем, полученным от Боба. Но если мы зашифруем публичным ключём, то Ева сможет легко его получить и сама расшифровать, верно?
Ещё для меня осталось непонятным, как можно зашифровать публичным ключём и расшифровать только секретным на стороне Боба. То есть зашифровали словом «Дом» , а расшифровали словом «Мир» . Для меня это какая-то несуразица.
Исходя из этих очевидных пробелов (или у вас, или у меня) , я сделал вывод , что тут схема должна быть посложнее, чем на картинке. Скорее всего под стрелочкой от публичного ключа Боба к Алисе имеется в виду другое, а именно вся последовательность действий по получению «Y» и «P», получению промежуточных результатов и тд. Иными словами , я думаю, что при шифровке исходного сообщения якобы публичным ключем, на самом деле шифруется не публичным, а уже секретным , который вычисляется на каждой стороне по отдельности.
Ещё у меня возник вопрос о расшифровки дважды зашифрованного сообщения. Если взять ,допустим, шифр Цезаря, где каждая буква шифруется другой буквой, стоящей , скажем, на 3 позиции дальше. Если Алиса зашифрует букву А в сообщении буквой Б, а потом Боб зашифрует эту букву Б буквой Г, то получить букву А из Г будет просто, причём в любом порядке. Правда это скорее всего будет работать только в тех случаях, если оба знают тип шифрации собеседника и при достаточно простых типах шифрации (моноалфавитные/полиалфавитные). Я тоже новичок в криптографии, так что это моё имхо ;)
Забыл ещё спросить.
В чём разница между симметричным и асимметричным способами?
Если я воспользовался алгоритмом Диффи и Хеллмана для передачи секретного ключа, а потом смог безопасно передать зашифрованное сообщение, то будет ли этот способ симметричным?
Я почитал, более менее как-то всё сгрупировал в уме.
Отвечу на вопросы мною написаные, возможно, помогая тем самым другим читателям.
1. По поводу
В этой статье упомянут алгоритм RSA. Алгоритм симметричного шифрования. В нём действительно используется следующий алгоритм:
1) Опираясь на некую одностороннюю функцию шифрования ( функция, которую легко посчитать в одну сторону, но очень трудно в другую. А) мы создаём на получателе пару {открытый ключ;закрытый ключ}. Эта пара уникальна, то есть каждому открытому ключу соответствует уникальный закрытый ключ под эту одностороннюю функцию.
2)Открытый ключ передаётся отправителю.
3)Отправитель шифрует сообщение
4)Передаёт получателю
5)Получатель дешифрует с помощью закрытого ключа. Это сообщение нельзя дешифровать с помощью открытого ключа.
Как видите, отправитель не знает закрытого ключа и он не в состоянии сам расшифровать своё же зашифрованное сообщение. Потому он и называется асимметричным, что у одного есть все ключи, а у другого только лишь часть, необходимая для шифрации.
Алгоритм Дэффи-Хелмана, который служит для обмена ключами и дальнейшим симметричным шифрованием. То есть его суть в том, что сначала оба получают полный ключ для шифрации и дешифрации и потом уже начинают самое обычное симметричное шифрование.
Асимметричный способ — у одного узла есть вся информация для шифр./дешифр., а у другого, как правило, только для шифрации
Симметричный — оба узла знают всю информацию для шифр./дешифр.
Надеюсь, что кому-то помог ;3
В этой статье упомянут алгоритм RSA. Алгоритм Асимметричного шифрования Опечатался.
Гм… только сейчас заметил ваши комментарии. Приношу свои извинения.
Все вроде верно. Есть одно но по вашему последнему абзацу, а конкретно термины:
Я все равно не понял утверждение:
2)Открытый ключ передаётся отправителю.
3) Отправитель шифрует сообщение
4)Передаёт получателю
5)Получатель дешифрует с помощью закрытого ключа. Это сообщение нельзя дешифровать с помощью открытого ключа.
Получается то, что Вы и мели ввиду с самого начала. Шифруем словом Дом, а дешифруем словом Мир. Означет ли это, что присутствует еще один алгоритм связующий Мир и Дом между собой ?
Не понял вопрос. В общих чертах это выглядит так:
Шифруем слово «Дом» словом «Мир», а дешифруем словом «Шар». Как то так.
Спасибо огромное!!!
Спасибо. Решил наконец разобраться, как это работает и понял из этой статьи. Только, я считаю, если сообщники знают друг друга и есть возможность обменяться безопасно открытыми ключами, то так и стоит сделать. Чтобы исключить пагубное воздействие возможного появления человека посередине при обмене ключами, который будет прикидываться А как Б и Б как А подменяя ключи на свои и просматривая в итоге всю информацию.
А в видео, думаю, зря они используют вот это вот 3^(24*54), т.к. вообще не очевидно откуда оно взялось, или пояснили бы, что это условно.
Ну если они имеют возможность безопасно обмениваться открытыми ключами, то ассиметричное шифрование в общем то здесь и не нужно. Достаточно установить один общий ключ шифрования, и им шифровать свои сообщения обычным симметричным шифром.
Ассиметричное шифрование, а конкретно приведенный в статье алгоритм, нужен для возможности передачи секретных сообщений по открытому каналу.
Спасибо за статью. Всё очень доступно разъясняется.
Ну раздражает ведь всех эта неграмотность правописания — «одностороняя» , «примененны», «длинна», как будто уж в 5-м классе. А так, неплохо для понимания основ.
Стыдно мне.
Когда пишу интересные тексты, начинаю абстрагироваться от самого процесса написания, и делаю много ошибок. А перечитывать что написал потом лень (
Бывает, что вопрос стоит просто. Вирусы-шифровальщики используют закрытый ключ. Есть оригинальный файл, есть файл зашифрованный. Задача: найти алгоритм, сказать так, который ищет алгоритм преобразования первого файла во второй…
Благодарю за понятную и нескучную статью! Наконец-то я врубился в основы :).
И вам спасибо за то что моя статья кому-то полезна :)
Это не совсем так. приведу пример:
— предположим что каждой букве соответствует цифровой код А = 1, Б = 2, В = 3 и т.д.;
— предположим что Алиса отправляет Бобу письмо, состоящее из единственной буквы А (для упрощения примера);
Алиса: накладывает свой шифр А + 2 = В
Алиса: отправляет письмо Бобу
Боб: накладывает свой шифр В + 3 = Е
Боб: отправляет письмо Алисе
Алиса: снимает свой шифр Е — 2 = Г
Алиса: отправляет письмо Бобу
Боб: снимает свой шифр Г — 3 = А
Здесь число 2 — секретный ключ Алисы, 3 — секретный ключ Боба. Причем он может быть и не односимвольным. В принципе его длина ничем не ограничена.
Ева перехватывает шифрованное сообщение, делает частотный анализ и по нему без труда получает расшифрованное сообщение, при этом не зная секретов Боба и Алисы
Я долго обходил стороной теоретические основы ассиметричного шифрования. Знал поверхностно — есть открытый ключ, которым шифруются данные, и есть закрытый, которым эти данные дешифруются. Но меня всегда напрягала мысль о реализации подобного шифрования.
Ваша статья во многом помогла, за это огромное вам спасибо!
Только к ее концу я опять увидел эту несуразицу — «шифруется открытым ключом». Ведь, строго говоря, шифруется сообщение не открытым ключом, а ключом, полученным на основе закрытого ключа отправителя и открытого ключа получателя (который, в свою очередь, был сгенерирован на основе закрытого ключа получателя). Ведь в таблице про Алису и Боба — они и только они смогли получить один и тот же ключ «9» — он и используется для шифрации и дешифрации сообщения. А вот получить этот ключ можно только на основе пары ключей — секретного (Алисы/Боба) и публичного(Боба/Алисы).
Образно — да, сообщение шифруется всегда секретным ключом отправителя (он, грубо говоря, постоянен) и публичным ключом получателя (он зависит от конкретного получателя), поэтому в описании шифрация «секретным» ключом опускается — и это опущение ломает всю стройность рассуждений.
прочел статью и не очень всеравно понял, хоть и лучше чем на вики. Но одно мне не понимается только. если ктот может ответить правильно — помогите.
если я всем посылаю вопрос «сколько будет 2+2?», рассказываю как зашифровать ответ мне (рассказываю всем публичный ключ), и все мне направят ответ на вопрос, как я узнаю того, от кого именно я жду ответа, тобиш того с кем я хотел установить связь на самом деле?
Тут вы немного неправильно ставите вопрос.
Если вам надо с кем то установить связь, то нужно идти от обратного. Вы подключаетесь к собеседнику, и уже он вам предоставляет свой публичный ключ, а не вы ему.
UPD: написал статью про цифровую подпись, я думаю это будет правильный ответ на ваш вопрос.
с моей тупостью придется повоевать. тема расжевана в коментариях и в вашей статье, кажется все обьяснили.
все же. зачем мне его публик ключ ? скажите если я не правильно понимаю.
я инициатор (мне нужны ответы, в примере я — принимающая сторона), значит генерирую пару. это ему, отвечающему (отправитель в вашем примере) нужен мой публик
Да, тут все верно. Будучи стороной принимающей соединение, при подключении клиента, вы ему отдаете свой публичный ключ. Он этим ключом шифрует сообщение. Сообщение зашифрованное вашим публичным ключом сможете расшифровать только вы своим приватным ключом.
Может быть эта картинка вам поможет понять принцип:

спасибо за вашу старательность ) разобрался. а мой первоначальный вопрос, на сколько я теперь знаю, был о электронных подписях не относящихся к алгоритму передачи ключей. спасибо за книжку, оч интересная
Хм… да может быть я вас не совсем верно понял изначально)
Несколько раз перечитал эту статью и другие по теме, непонятен алгоритм использования ЭЦП в эл. документах. Если так как здесь: https://ru.wikipedia.org/wiki/Электронная_подпись, то возникают расхождения. Так все таки шифруем с помощью закрытого ключа или открытого?
Если мы что то подписываем, то подпись формируем на основе нашего закрытого ключа. А наш публичный ключ должен быть у получателя, с помощью него он сможет эту подпись расшифровать.
Если подпись «расшифровалась», то значит публичный ключ соответствует закрытому, а т.к. закрытый ключ априори имеется только у отправителя, то значит подписал документ именно отправитель.
Дмитрий, мне очень помогла ваша статья, у вас хороший стиль. Но есть непонятный момент, вы утверждаете, что асимметричный алгоритм предполагает под собой наличие двух ключей – публичного и приватного. То есть сообщение шифруется публичным ключем, а расшифровывается приватным и ни как иначе.
Может быть дело в исходных задачи, например получателю нужно аутентифицировать посланника.
Тогда не представляю как эта схема может помочь?
Не совсем верно. Сообщение шифруется одним ключом, а расшифровывается другим. Т.е. вполне можно зашифровать приватным, а расшифровать публичным.
Давайте рассмотрим на примере. Вы хотите мне прислать сообщение, я хочу убедится что прислали его мне именно вы. Поэтапно:
1) Вы шифруете сообщение закрытым ключом
2) Присылаете его мне
3) Я обращаюсь к вам, и получаю от вас Ваш публичный ключ
4) Полученное сообщение расшифровываю Вашим публичным ключом
5) Если сообщение расшифровалось — значит послали его именно вы
Никто другой не сможет послать это сообщение, представившись вами, потому что приватный ключ есть только у вас.
Ок, но как быть если требуется скрыть от любопытных глаз сообщение?
Ну с этим тоже ничего сложного
1) Вы шифруете сообщение закрытым ключом
2) Обращаетесь ко мне за моим публичным ключом
3) Шифруете еще раз но уже моим публичным ключом
4) Присылаете его мне
5) Я обращаюсь к вам, и получаю от вас Ваш публичный ключ
6) Полученное сообщение расшифровываю своим закрытым ключом
7) И еще раз расшифровываю уже Вашим публичным ключом
8) Если сообщение расшифровалось – значит послали его именно вы
Это конечно утрировано. В качестве подписи шифровать документ целиком смысла особого нет, можно зашифровать хеш от него, который уже приложить к пересылаемому документу, что в общем то и будет являться подписью. На стороне получателя расшифровываем подпись вашим публичным ключом, и сравнить хеш документа с полученным хешем. Но это уже детали реализации.
Наверное лучше бы это нарисовать, но признаюсь честно, мне немного лениво)
Благодарю за ответы, могу задать еще вопрос: вам не приходилось работать с JWT: http://jwt.io/ ?
Нет, с этим работать не приходилось
Добрый день! Статья понравилась, но остались вопросы (даже нашлась пара похожих в комментариях, но без ответов).
Если во второй части статьи всеже перейти к аналогии с Алисой и Бобом, в частности к числам А, В, а, в, Р и к полученному в примере числу 9, что из них будет закрытым ключом, а что открытым? Заранее спасибо за ответ!
Не понятно, отправился мой комментарий или нет :(
Отправился, я комментарии проверяю сначала перед публикацией. А то спамить любят тут у меня :) Секунду сейчас на предыдущий ваш вопрос отвечу
Правильнее будет сказать что в процессе обмена данными Алиса и Боб получают общий ключ 9, который в дальнейшем могут использовать для шифрования своих сообщений. По сути в статье я описывал не само ассиметричное шифрование как таковое, а протокол обмена ключами, который дал толчок к развитию ассиметричного шифрования.
Алгоритм генерации пары приватный/публичный ключ на самом деле немного сложнее, хотя и похож на выше изложенный алгоритм, но все таки наверное стоит отдельной статьи. В комментарии я не распишу тут сходу, ибо могу много чего напутать.
Поняла, еще раз спасибо за статью, она разъяснила достаточно много непонятных моментов!;)
И вам спасибо за отзыв, заходите почаще :)
Как ни странно, но ева быстро решит задачу где
5 в стенени x (mod 7) ===2, и при огромных числах. Почему? Потому что возведение в степень это быстро. И вычисление по модулю тоже. А значит и перебор всех значений не займет много времени. Считаю это слабым местом.
Вы не совсем верно поняли принцип. Задача в другом, грубо говоря, Еве предстоит определить какое число следует возвести в степень X чтобы получить остаток по модулю два. Или же в какую степень нужно возвести число X. Это решается по сути только перебором, да и найденных решений будет очень много, которые тоже надо будет перебирать. В принципе пока это все звучит довольно просто. Но вот в серьезных алгоритмах используются числа с порядком в несколько сотен, а вот это уже не совсем просто :)
Когда то давно, думали что md5 сложно прокрутить перебором, чтобы узнать исходный текст. Но теперь даже исходные длинные строки раскрываются быстро. Есть сайты, где Вы пишите хэш, а вам через некоторое время Вашу исходную строку. Секрет прост -заранее на суперкомпьютерах сп_цсл_жбы готовят таблицы соответствий. То есть, например, исходная строка до 20 символов распознаются мгновенно если имеется только её md5 хэш. Суперкомпьютеры круглосуточно эти таблицы составляют. Даже в эту минуту, когда Вы читаете этот текст. Та же участь ждёт и все сокрытия в степени по модулю. И в том числе и поиск множителей простого числа. Заранее. Выход — собственно доразработанная система шифрования + очень уж длинные ключи. Но тогда при формировании рукопожатия будет много времени уходить.
Это называется борьба щита и меча.
Сейчас вместо md5 рекомендуют использовать sha. Когда устареет sha, придумают что то новое. Так же и с шифрованием.
Где-то через двадцать лет всё равно придётся отказаться от ассиметричной классической криптографии, потому что к тому времени построят мощный квантовый компьютер, и разложение на множители, поиск дискретного логарифма и т.п. станут тривиальным делом
За статью огромное спасибо. Я вот тоже не пойму. Формула общеизвестная. Y^X mod P, где Y и P известны. Осталось вычислить P. Достаточно перехватить результаты (что довольно легко для спецслужб), как в примере Y^X mod p = 2 и Y^X mod p = 4, где 2 и 4 по сути публичные ключи. И вычислить 7^X mod 11 = 2 и 7^X mod 11 = 4 перебором это easy. Тут скорее уже другой вариант надо использовать, который на эллиптических кривых.
Кстати, помечу вы посоветовали мутную книгу какого-то Сигха вместо классической книги Шнайера «Прикладная криптография»? Шнайеровская книга — это просто классика криптографии, написанная в 90-е годы, она всё равно является очень хорошим учебником. После неё можно почитать «Практическую криптографию» того же автора — она более новая и лаконичная
Оу… «мутную книгку» и «какого-то Сингха», это вы зря) Очень хорошая книга, хорошо читается, и очень хорошо разжевывается материал. Рекомендую.
Вот я зря говорить не буду — я пробовал. Прочитал несколько страниц и бросил, ничего не поняв. Вот Шнайер — другое дело — просто и с юмором
Видимо все таки на вкус и цвет как говорится. Надо будет вашего Шнайера глянуть.
Все таки заставил я себя начать читать Шнайера. Я бы сказал, что его стоит читать после Сингха. У Сингха по сути разжевываются основы, история зарождения и развития криптографии, и простейшие алгоритмы. Шнайер намного более «профессионален», если можно так сказать. Знания он дает более углубленные, и вопрос нужно ли оно новичку или нет.
Спасибо вам большое за статью. Именно так должны объясняться любые вопросы: простыми словами о сложном. К сожалению, не многие обладают талантом объяснять сложные вещи на простых, более понятных простому человеку, аналогиях. Теперь я знаю, что такое ассиметричное шифрование.
Best regards from Berlin.
Благодарю вас за теплые слова :)
У меня вот возник вопрос: «А как применить такое на практике?». Давайте в качестве примера возьмем SSH-соединение с публичным ключом. Насколько я понял, публичный ключ — шифрует, закрытый ключ — расшифровывает. Окей, тут все понятно. Теперь, я собираюсь создать защищенное соединение с Алисой. Для этого я посылаю ей сгенерированный мною публичный ключ, а секретный держу при себе. Она с помощью моего публичного ключа шлет мне зашифрованное сообщение, я его на своей стороно расшифровываю. Хорошо. Но ведь это одностороннее шифрование. Как же мне отвечать Алисе зашифрованными сообщениями? Неужели Алисе тоже придется создать свой публичный ключ и отправлять его мне, чтобы я мог шифровать свои сообщения?
Заранее спасибо :)
Тимур, вариантов на самом деле масса. По канону асимметричной криптографии, конечно, у обоих сторон должна быть пара приватный/публичный ключ.
Но на самом деле, в принципе, это необязательно. Например как вам такой алгоритм:
1) Вы шлете Алисе публичный ключ.
2) Алиса генерирует какой либо сеансовый ключ, сохраняет его у себя
2.1) Алиса шифрует этот же сгенерированный сеансовый ключ вашим публичным ключом, отправляет вам
3) Вы расшифровываете его приватным ключом
В итоге две стороны имеют у себя сеансовый ключ. Этот ключ используется в виде обычного ключа для обычного симметричного шифрования. Все последующие сообщения между вами и Алисой вы шифруете и расшифровываете именно им. В итоге получается что только одна сторона должна генерировать ключи. А также симметричное шифрование которое будет использоваться для фактического обмена сообщениями намного менее ресурсоемко. В общем одни плюсы)
Вообще тот же SSL и работает приблизительно по такому принципу.
Уважаемый Дмитрий!
Великолепный ход Ваших мыслей просто завораживает, однако исходя и алгоритма приведенного Вами в примере, хотелось бы уточнить, но подобрать степень под результат простым перебором вариантов это же возможно, хотя бы теоретически, либо я что то не полностью понял в абсолютной стойкости такого принципа, Спасибо за ранее за Ваш ответ
С уважением Евгений.
Евгений, вчера набирал вам здоровенную простыню текста с ответом. А сейчас обнаружил, что я видимо забыл его сохранить. Обидно… Попробую еще раз.
Да, простым перебором подобрать можно. Но задача в том чтобы подобрать две неизвестные x и y в уравнении вида 4x (mod 11) = 2y (mod 11) (взял из текста статьи). Для такого уравнения это выглядит бесспорно просто, но в реальности используются числа сотен порядков, и боюсь простой перебор реальных чисел займет лишь немногим меньше вечности.
В криптографии алгоритм называется стойким если он взламывается только полным перебором ключей. Естественно с маленькой оговоркой на то что такой перебор будет занимать огромное количество времени.
Так что, в принципе, этот шифр можно назвать стойким.
Дмитрий! Большое Вам СПАСИБО за Ваш ответ, великолепно!, однако, как я заметил, в итоге обмена между контрагентами, они вычисляют закрытый ключ он одинаков в результате у Алисы и Боба это в Вашем примере 9, и это абсолютно верно, но в таком случае это одинаковый код т.е. ключ для шифровки текста и дешифровки оба участника имеют идентичный ключ, прошу поправить, если ч не прав …
С Уважением, Евгений
Евгений, все верно. В тексте статьи я, откровенно говоря, немного слукавил)
В статье описан протокол согласования ключа Диффи-Хелмана. Этот протокол дал начало асимметричной криптографии, и таким протоколам как RSA и т.д, т.е. тем протоколам где используются открытые и приватные ключи в общем их понимании. Но основы и математика у всех асимметричных алгоритмов схожи. А протокол Диффи-Хелмана наиболее прост для понимания.
Уважаемый Дмитрий!
Ваш ответ исчерпывающий, ход Ваших мыслей и логика великолепны.
С уважением, Евгений.
Алгоритм Диффи-Хеллмана.
Зачем Еве вообще знать секретные числа?
Ева берёт открытый ключ 7^x mod 11.
Перехватывает a и b.
Получает A и B.
Например, мы перехватываем a=10, b=6. 7^A mod 11=10 => 7^5 mod 11=10
Получаем A=5;15… , B=7;17…
Не зависимо от того, какие секретные числа выбрали Алиса и Боб, мы получим одинаковый ключ.
6^5 mod 11 = 10; 10^7 mod 11=10;
6^15 mod 11 = 10; 10^17 mod 11 =10;
И о какой шифрации идёт речь?
Сергей, вы ловко подменяете понятия вот в этом месте:
Числа A и B вы можете получить только полным перебором. И для таких маленьких чисел это бесспорно просто. В реальных алгоритмах используются числа сотен порядков. Боюсь что их подобрать у вас попросту не выйдет.
Приведите пример, пожалуйста, реально используемых чисел.
Если брать например 7^400 mod 11, то вычисление на листке бумаги займёт секунд 30.
Вы наверное не правильно поняли мою фразу про насколько сотен порядков. В реальном алгоритме Диффи Хелмана, используются ключи минимум в 512 бит, а это число с где-то 150 нулями (и то это уже совсем не секурно, стараются брать 1024 или 2048бит).
Для понимания масштабов, пара 1024битных ключей, в 16ном виде:
Дмитрий! Поясните пожалуйста, в Вашем примере значение p это один символ имеющий многоразрядное значение т.е. значение p = коду состоящему из множества цифр?
Не понял ваш вопрос. Это просто число представленное в 16-ричной системе счисления. Первое которое я нагуглил)
Дмитрий! Я хотел спросить, в Вашем примере, если число обратно из 16 — ричной системы, перевести в десятичную, то получится очень большое значение, то есть очень большое число?
Да, очень большое значение, порядка 1.5632008148827224e+308, если вам такая запись будет удобнее) Проще говоря число с 300 нулями.
Да именно так я и понял Ваш пример, в таком случае перебор таких чисел с учетом того, что шифруется каждая буква текста, то может занять вечность -:)
Уважаемый Дмитрий! Я проанализировал аргументы, приведенные в примере Вашим собеседником Сергеем.
С приведенными Сергеем выводами я не согласен, поскольку он не предоставил факты: — каким образом он получи секретные числа Алисы и Боба, а лишь просто подставил их в функцию.
В результате я пришел к выводу, что Сергей заблуждается, либо как Вы верно указали происходит подмена понятий, таким образом получить ключ действительно возможно, но лишь только перебором всех искомых вариантов, либо это просто угадывание, а проще говоря, подгонка неизвестных под требуемый ответ.
Однако я обратил внимание на интересную деталь, которая содержится в примере Сергея, а именно, что кроме секретных чисел Алисы и Боба, это числа 5 и 7 в примере Сергея, результат 10 дают также числа: 15; 17 и т.д. 25;27, 35;37 …
Я думаю, что это значит, что такая функция циклична.
Исходя из такой вот дискуссии, порошу Вас изложить Вашу позицию.
С уважением, Евгений.
Евгений, вы задали очень хороший вопрос. Боюсь, что сходу я не смогу на него ответить. Для ответа нужно иметь математические знания и полное представление алгоритма, а у меня это все уже давным давно выветрилось из головы…(
Уважаемый Дмитрий!
Я Вам искренне признателен за Ваш ответ, в любом случае, приоритет всегда за Вами, вне зависимости от чего либо, как бы то ни было, мне очевидна ясность и логика ваших мыслей, и это главное, я не просто так Вам задал вопросы, прошу меня простить, если что, просто я привык доводить дело до логической развязки, я проанализировал Вашу функцию, приведенную в примере, а также сопоставил информацию из ролика который у Вас тут на ресурсе данной статьи, в нем есть пример часового алгоритма, я изложу Вам свою позицию, но я тоже беру тайм-аут для обработки данных.
С уважением Евгений.
Уважаемый Дмитрий!
В Вашем примере Боб получает a от Алисы, и вычисляет значение aB (mod 11) = 26 (mod 11) = 64 (mod 11) = 9
при этом, 6 является секретным числом Боба (B)
Как следует из поясняющего видео к данной теме, цифра 2 является генератором, возводя его в любую степень по модулю 11 мы получим в итоге набор чисел от 1 – 10
в непоследовательном порядке, далее, как и в примере из ролика разложим значения по часовому циферблату в данном случае на нем будет 10 чисел, и в зависимости от степени возведения стрелка часов будет указывать нам результат от 1 до 10 и так в замкнутом порядке, т.е. результат вычисления по модулю 11 будет повторяться через каждые 10 единиц, к примеру цифры 2;12;22;32… дадут результат 4, цифры 6;16;26;36 … дадут результат 9
Ниже приведены функции:
2^1 mod 11 2
2^2 mod 11 4
2^3 mod 11 8
2^4 mod 11 5
2^5 mod 11 10
2^6 mod 11 9
2^7 mod 11 7
2^8 mod 11 3
2^9 mod 11 6
2^10 mod 11 1
2^11 mod 11 2
2^12 mod 11 4
2^13 mod 11 8
2^14 mod 11 5
2^15 mod 11 10
2^16 mod 11 9
А если разобрать сам пример из видеоролика там функция
3^x mod 17, в данном примере повторение результата будет происходить через 16 единиц,
например, функция вернет нам число 15 по модулю 17 при возведении 3 в степень 38;54;70;86;102
Ниже приведены функции:
3^38 mod 17 … 15
и далее
3^54 mod 17 15
3^55 mod 17 11
3^56 mod 17 16
3^57 mod 17 14
3^58 mod 17 8
3^59 mod 17 7
3^60 mod 17 4
3^61 mod 17 12
3^62 mod 17 2
3^63 mod 17 6
3^64 mod 17 1
3^65 mod 17 3
3^66 mod 17 9
3^67 mod 17 10
3^68 mod 17 13
3^69 mod 17 5
3^70 mod 17 15
3^71 mod 17 11
3^72 mod 17 … 16
и далее
3^86 mod 17 … 15
и далее
3^102 mod 17 … 15
Думаю вышеизложенная информация может доказывать, что такая функция циклична, на величину своего модуля, точнее на одну единицу меньше, т.е. по mod 11 решения будут от 1 до 10, по mod 17 от 1 до 16.
С уважением, Евгений.
Уважаемый Дмитрий!
Ваше мнение, мне очень важно, и интересно, прошу Вас изложите, пожалуйста, СПАСИБО!
С уважением, Евгений.
Евгений, я знаю что вам интересно мое мнение) Извините что никак не отвечу вам до сих пор. Мне нужно собраться с мыслями и разобраться с вашим примером и алгоритмом в целом, не могу никак выделить на это свое время. Обещаю что постараюсь это сделать в ближайшем будущем.
Дмитрий!!!
Я Вас понял, в таком случае слово за Вами …
Дмитрий вы упустили очень важный момент. Для того, чтобы задача была трудно разрешимой, число P должно быть ОЧЕНЬ БОЛЬШИМ ПРОСТЫМ ЧИСЛОМ, и 11 на эту роль подходит плохо.
В практических реализациях используются P порядка 10 в 300 степени.
Добрый день Андрей!
В Вашем замечании Вы указываете на то, что число P должно быть очень большим простым числом, число 11 из примера Дмитрия простое число по определению, простое поскольку, число 11 целое положительное и делится без остатка только на 1 и на само себя, ну и конечно же оно маленькое, в силу тех обстоятельств, что это всего лишь пример, для внесения ясности в логическое изложение принципа заложенного в алгоритме.
Привет Дмитрии,
Привет очень познавательная статья.
Завут Костя . Сам я из Молдавии, работаю в Барселоне девелопер.
Удачи в дальнеишом!
Привет Костя! Удачи и успехов тебе тоже.
Хорошая работа. Прояснил наконец для себя этот вопрос. Добавил в избранное.
В конце надо было еще дать ссылку на документацию протокола TLC (тут на русском https://tls.dxdt.ru/tls.html), т.к. мало знать алгоритма, много чего еще происходит за кулисами в реальности. (:
Автор, большое спасибо за статью! Тот, кто способен простым языком объяснить сложные вещи — и есть настоящий профессионал!
Прекрасная статья, отлично и понятно описанны логика ассиметричного шифрования , долго промучился с поиском такой внятной статьи.Пишите чаще,будем поддерживать ваши труды.
Искренняя признательность и благодарность автору.
С уважением Алексей.
Благодарю. Ваши комментарии — лучшая поддержка для меня! :)
Дмитрий, здравствуйте!
присоединяюсь к похвалам по поводу стиля вашего изложения материала — он соответствует по ясности англоязычным учебникам по трудным дисциплинам :)
Меня очень зацепили слова из вашего текста:
Я не побоюсь сказать: за последние два дня я такой алгоритм придумал. Спасибо за постановку задачи, вы — соучастник :)
Спасибо за теплые слова =)
Насчет алгоритма, тут двое участников выше уже отписывались, что так же придумали такие же алгоритмы. Только на поверку они оказались абсолютно бессмысленными так как стойкости ко взлому у этих алгоритмов просто нет.
Я это отследил быстро.
Перехватив все три сообщения человек-в-середине мог бы восстановить ключи простыми алгебраическими операциями. Но. Мы тоже не лыком шиты.
Я добавил неопределенности и таким образом повысил стойкость.
Человек-в-середине, перехватив все три сообщения, может по ним методом перебора найти верные ключи, но такой перебор займет слишком много времени.
Как протестировать или даже померить стойкость — не знаю/не умею:)
Аналогию с цветами понял, математику — нет. Гуманитарий, что тут скажешь.
Дмитрий,
Отличная статья! Все разложено доступным языком. Спасибо!
Замечательная статья!!! Спасибо! Все написано доступно и очень интересно=)
Здравствуйте! Немного не понятно в последовательности:
В пункте 3, как понять обращаюсь, т.е. нужно чтобы свой публичный ключ мне прислал человек по электронке? Так что ли?
Я не понимаю почему 3^(24*54) mod 17 = (3^24 mod 17)^54 mod 17
Тот же вопрос. Может вы уже разобрались?
В математике будущего нет такого понятия необратимая функция «смешанную краску разделить на первоночальные цвета Еве удасться» Потому что она знает один из цветов:желтый. Если бы вместо краски была нефть смешанная с водой, электролиз разделит воду и нефть.Фантастика? Нет после того, как математичка решила задачу с диффузией сахара в чае.
Здесь описаны не «необратимые» функции, а односторонние. Это те, для которых сложность вычисления прямого и обратного значения сильно различаются. Собственно, их существование на данный момент не доказано и не опровергнуто, но принято пользоваться допущением, что они существуют (подобное происходит с гипотезой Римана).
Огромное спасибо. Наконец-то впервые лет этак за 10 я все по этой теме уяснил.
Обновите пожалуйста видео. А статья супер!
Очень хорошо написано, сразу все стало понятно :) спасибо за статью!
статья супер!
по методу: если на почте Бобу под видом «замок Алисы» дадут «замок Евы», то Ева перехватив послание сможет его открыть своим ключом. Так что безопасность под сомнением.
64 (mod 11) = 5 а не 9
64 (mod 11) = 9 а не 5
посчитайте внимательней.Все ошибаются 64 mod 11 = 9
mod — остаток от еления. Т.е. (11*5)+9=55+9=64. Т.е. 64 mod 11 = 9
Ты такой странный !!!
Описание RSA ничем не сложнее протокола Диффи-Хеллмана в плане использования математического аппарата.
Ты привёл описание для Диффи-Хеллмана, но отказался расписать RSA, хотя там те же функции и понятия используются. Это очень странно выглядит со стороны.
спасибо ,хорошее погружение!!
Спасибо за статью
Подскажите, пожалуйста, какую роль играет пароль к ключу шифрования? Например, в truecrypt или pgp предлагается защитить ключ дополнительно паролем. Он шифрует ключ, или дополняет его? Насколька велика опасность если ключ скомпроментирован но пароль от него не известен злоумышленнику?
Без пароля от ключа злоумышленник не сможет им воспользоваться. Т.е. да, пароль фактически защищает ключ от непреднамеренного использования, но не дополняет/усиливает его.
Ещё актуально в 2020м)
Еще кватновых компьтеров нет, значит актуально.
Очень интересная статья, очень понятная… Спасибо автору
1. Алиса — 1л жёлтой краски , Боб — 1л жёлтой краски
2. Алиса — 1л Жёл + 1л Зел краски, Боб — 1л жёл + 1л Син
3. Обмен: Алиса — 1л Жёл + 1л Зел Боб — 1л жёл + 1л Син =
Боб — 1л Жёл + 1л Зел , Алиса — 1л жёл + 1л Син
4. Боб добавляет секретную краску (Гол) , Алиса добавляет ( чёр)
5. В Результате у Боба находится 1л Жёл+1л Зел+1л Гол
6. В результате у Алисы находит 1л Жёл+1л Син+1л Чёр
С чего вдруг написано, что у них краска в банках стала одинакового цвета?
«Но суть в том что не существуют таких шифров, которые бы позволили снять шифр из под другого шифра.»
Уже существует… :)
Скоро выложу на гитхаб…
Шифрование это независимый участок кода и там же и ключ есть?
31.20.33.43.19.24.32.7.33.39.26.39.34.30.27.36.35.21.40.31.30.33
То есть сели завели и поехали?